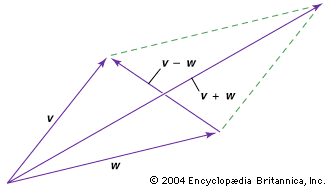
The combination (v+w)/2 is invariant to switching v and w and is therefore termed symmetric. Lets call it s so that s=(v+w)/2. Graphically s can be drawn pointing from the origin to the point midway between the terminal points of vectors v and w. We can think of it as the average vector.
The combination (v-w)/2 reverses sign by switching v and w and is therefore termed antisymmetric . Lets call it a so that a=(v-w)/2. Graphically a can be drawn pointing from the terminal point of s to the terminal point of v. Similarly -a is the vector pointing from the terminal point of s to the terminal point of w. We can think of it as the difference vector.
This is a nifty representation since v=s+a and w=s-a. To interpolate between v and w we need only vary the parameter t from -1 to 1 in the expression s+t*a. Of course there is a max patch that demonstrates this. You must save and reopen this patch to get it to initialize properly.
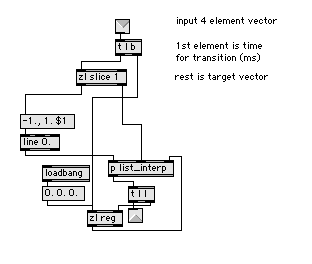Happy interpolating! Code in the comments section.
1 comment:
#P window setfont "Sans Serif" 9.;
#P window linecount 1;
#P newex 106 104 51 196617 zl slice 1;
#P newex 72 200 48 196617 loadbang;
#P newex 158 221 27 196617 t l l;
#P message 50 149 55 196617 -1. \, 1. \$1;
#P newex 50 169 40 196617 line 0.;
#P message 72 221 43 196617 0. 0. 0.;
#P newex 145 74 27 196617 t l b;
#P newex 117 245 36 196617 zl reg;
#N vpatcher 532 244 1132 644;
#P window setfont "Sans Serif" 9.;
#P window linecount 0;
#P newex 38 42 114 196617 loadmess scalarmode 1;
#P inlet 299 25 15 0;
#P inlet 213 27 15 0;
#P window linecount 1;
#P newex 128 148 107 196617 vexpr ($f1 + $f2)/2.;
#B color 5;
#P newex 211 77 91 196617 vexpr ($f1 - $f2);
#B color 5;
#P newex 225 50 92 196617 vexpr ($f1 + $f2);
#B color 5;
#P newex 128 123 93 196617 vexpr ($f1 * $f2);
#B color 5;
#P inlet 128 103 15 0;
#P outlet 128 170 15 0;
#P toggle 50 79 15 0;
#P message 50 99 74 196617 scalarmode \$1;
#P connect 1 0 0 0;
#P connect 3 0 4 0;
#P connect 10 0 4 0;
#P fasten 0 0 4 0 55 119 133 119;
#P connect 4 0 7 0;
#P connect 7 0 2 0;
#P connect 8 0 6 0;
#P connect 6 0 4 1;
#P connect 8 0 5 0;
#P connect 5 0 7 1;
#P connect 9 0 6 1;
#P connect 9 0 5 1;
#P pop;
#P newobj 138 195 66 196617 p list_interp;
#P comment 203 50 111 196617 input 4 element vector;
#P window linecount 2;
#P comment 203 75 100 196617 1st element is time for transition (ms);
#P window linecount 1;
#P comment 202 106 100 196617 rest is target vector;
#P inlet 145 54 15 0;
#P outlet 158 243 15 0;
#P fasten 6 0 5 2 122 265 211 265 211 191 199 191;
#P fasten 13 1 5 1 152 159 171 159;
#P connect 11 0 0 0;
#P fasten 5 0 11 0 143 216 163 216;
#P connect 1 0 7 0;
#P fasten 11 1 6 1 180 240 148 240;
#P fasten 9 0 5 0 55 190 143 190;
#P fasten 7 1 6 0 167 132 122 132;
#P fasten 8 0 6 0 77 240 122 240;
#P fasten 7 0 13 0 150 96 111 96;
#P connect 12 0 8 0;
#P connect 10 0 9 0;
#P fasten 13 0 10 0 111 129 55 129;
#P window clipboard copycount 14;
Post a Comment