Symmetric Antisymmetric Interpolation

Given two vectors, v and w, we can linearly combine them to yield their symmetric and their antisymmetric combinations using vector addition and subtraction.
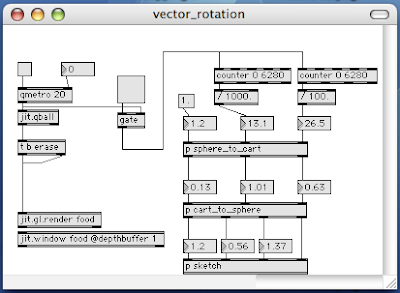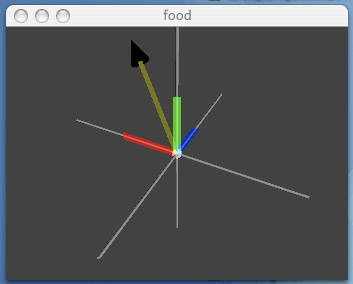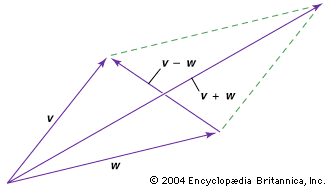
The combination (v+w)/2 is invariant to switching v and w and is therefore termed symmetric. Lets call it s so that s=(v+w)/2. Graphically s can be drawn pointing from the origin to the point midway between the terminal points of vectors v and w. We can think of it as the average vector.

The combination (v-w)/2 reverses sign by switching v and w and is therefore termed antisymmetric . Lets call it a so that a=(v-w)/2. Graphically a can be drawn pointing from the terminal point of s to the terminal point of v. Similarly -a is the vector pointing from the terminal point of s to the terminal point of w. We can think of it as the difference vector.

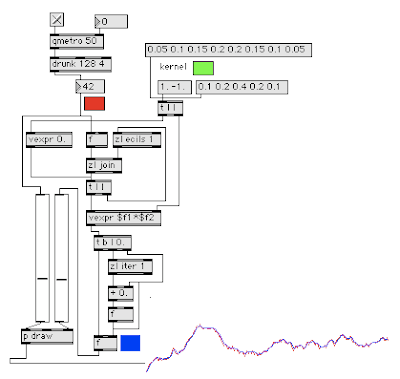
This is a nifty representation since v=s+a and w=s-a. To interpolate between v and w we need only vary the parameter t from -1 to 1 in the expression s+t*a. Of course there is a max patch that demonstrates this. You must save and reopen this patch to get it to initialize properly.
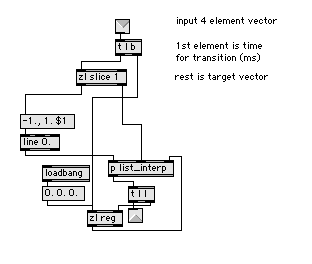Happy interpolating! Code in the comments section.

Space Cadets

Learning to navigate the force fields of deep space takes practice. A kinesthetic and mathematical understanding of an expressive instrument enhances its creative possibilities.

Music: Cops at the Door by Die Kapitalist Pig
Duck: Jon Kinzel
Biplane: Cavin Moore
Moonbug: Sarah Rosner
Cruiser: Meghan McCoy

Rotation

With vector vectoria Matt brings us from vectors to rotations, another vector quantity. Rotations play part in some of the deeper mysteries of physics. In OpenGL rotations determine the orientation of a graphical object. Here is a 3-D vector toy. The code is in the comments section. The patch has rotations going all over the place. Using a spherical coordinate system makes it possible to generate these rotations in q (theta) and f (phi). In the guts of the patch the orientation of the graphic arrow model is determined by using theta and phi as euler angles.

Vectors

A vector is a line from a point in space to another point in space. It has both magnitude and direction. Bound vectors begin at the origin and are determined by the location of the terminal point. There are many different ways to represent vectors.Cartesian coordinates present the most straightforward means of representing a vector. In cartesian coordinates vectors can be added and subtracted by adding and subtracting their respective x, y and z coordinates.Physical quantities such as force, acceleration, velocity and displacement are all vector quantities. In the gravity simulator we dealt with all 4 of these in their 2-D vector form. We also are dealing with vectors when extraction accelerometer data from the Wii remote.

Spherical Coordinates

Spherical coordinates provide another system for describing locations in 3-D. It uses the coordinate r, q (theta) and f (phi). Like polar coordinates it makes use of a radial coordinate. The length of the line joining the point to origin is the coordinate r. This same line subtends an angle q (theta) with the y (up/down) axis. As in the cylindrical system f (phi) determines the angular coordinate in the x-z plane. This is often referred to as the azimuthal coordinate.
Here is a patch that lets you play with 3-D spherical coordinates. The code is in the comments section. Since it uses cartesian coordinates we translate from spherical to cartesian as we send messages to OpenGL.

Here is how spherical and cartesian coordinates are related:

x = r cos(q) cos(f)
z = r cos(q) sin(f)
y = r sin(q)

Cylindrical Coordinates

Cylindrical coordinates specify a point in 3-D with a mix of polar coordinates and cartesian. Polar coordinates use a distance and angle measure to locate points in 2-D. Cylindrical coordinates use an additional distance measure to locate points in 3-D. For this example r and f are two polar coordinates and y is the third. We can translate from cylindrical to 3-D cartesian coordinates using r and f to determine x and z and using y as it is given.
Here is a patch that lets you play with 3-D cylindrical coordinates. The code is in the comments section. Since it uses cartesian coordinates we translate from cylindrical to cartesian as we send messages to OpenGL.

Polar Coordinates

The polar coordinate system is another way of keeping track of points on the plane. Instead of using Descartes' x and y coordinates to determine the position of a point we use r and q. The polar coordinate system is based on a line drawn from the origin of coordinates to the point. The length of this line is r. The angle between the line and the x-axis is q.
The mathematical relationship between cartesian and polar coordinates goes as follows.

x = r cos(q)
y = r sin(q)

The objects cartopol and poltocar convert between cartesian and polar coordinates. The angle is measured in radians. The code is in the comments section.
Lots of very exciting mathematics surrounds this relationship between polar and cartesian coordiantes by way of exponentials and complex numbers. One such jewel is Euler's formula.

Coordinates in OpenGL

Here is a patch that lets you play with a 3-D Cartesian coordinate system using OpenGL.
OpenGL uses Cartesian coordinates x, y, z for placement of objects, light source, viewpoint and focus point. The code is in the comments section.

Cartesian Coordinates

Coordinate systems allow us to refer to points in space using numbers. There are different kinds of coordinate systems and they can have different numbers of dimensions. A very familiar coordinate system is the 2-D Cartesian coordinate system.
In this coordinate system two numbers, x and y, specify a point in a plane. The name Cartesian comes from Descartes who is said to have "invented" the system while laying in bed sick and watching a fly crawl across the tiled ceiling.

The above 2-D Cartesian system can be expanded into a 3-D cartesian if we simply add a third dimension, z. As x determines the left/right position and y determines the up/down position the additional coordinate z determines the back/forth position.

Convolution

Convolution is one of the jewels of Fourier analysis.
It is the Fourier transform of the multiplication operator and useful in physics and signal processing.The integral equation for using the quantum mechanical propagator K reduces to a convolution if it depends only on relative differences in space and time. K=K(x-x',t-t')Here is a patch using convolution with a drifting time series and a set of different kernel functions. The output time series is the convolution of the input time series and the kernel function. Click on all of the different kernel functions to see how they change the output signal.
We are colonizing a field. Source code in comments section.

Player Participate

Gondry's film and installation at Deitch Projects, Be Kind Rewind, presents a refreshing view of culture, putting value on process and participation over product and profit. Making computer games out of ourselves, our movement vocabularies and the environments we inhabit, follows this same philosophy.

“I don’t intend nor have the pretension to teach how to make films. Quite the contrary. I intend to prove that people can enjoy their time without being part of the commercial system and serving it. Ultimately, I am hoping to create a network of creativity and communication that is guaranteed to be free and independent from any commercial institution.”-Michel Gondry

nice moves: Cavin Moore
nice music: Real Nice by Should Have Thought of That

Think Tank

Discourse is a dance. Sometimes it feels fun, sometimes dangerous. Here is the artifact from friday's think tank. We can learn from the content and form of such improvisations, improving our communications by getting rid of the bad style and keeping the good.

Click To Play